Deep Metric Learning (DML) aims to learn representation spaces on which semantic relations can simply be expressed through predefined distance metrics. Best performing approaches commonly leverage class proxies as sample stand-ins for better convergence and generalization. However, these proxy-methods solely optimize for sample-proxy distances. Given the inherent non-bijectiveness of used distance functions, this can induce locally isotropic sample distributions, leading to crucial semantic context being missed due to difficulties resolving local structures and intraclass relations between samples. To alleviate this problem, we propose non-isotropy regularization (NIR) for proxy-based Deep Metric Learning. By leveraging Normalizing Flows, we enforce unique translatability of samples from their respective class proxies. This allows us to explicitly induce a non-isotropic distribution of samples around a proxy to optimize for. In doing so, we equip proxy-based objectives to better learn local structures. Extensive experiments highlight consistent generalization benefits of NIR while achieving competitive and state-of-the-art performance on the standard benchmarks CUB200-2011, Cars196 and Stanford Online Products. In addition, we find the superior convergence properties of proxy-based methods to still be retained or even improved, making NIR very attractive for practical usage.
Introduction
Deep Metric Learning (DML)
Visual similarity plays a crucial role for applications in image & video retrieval, clustering, face re-identification or general supervised and unsupervised contrastive representation learning. A majority of approaches used in these fields employ or can be derived from Deep Metric Learning (DML). DML aims to learn highly nonlinear distance metrics parametrized by deep networks that span a representation space in which semantic relations between images are expressed as distances between respective representations.
Proxy-based DML
In the field of DML, methods utilizing proxies have shown to provide among the most consistent and highest performances in addition to fast convergence. While other methods introduce ranking tasks over samples for the network to solve, proxy-based methods require the network to contrast samples against a proxy representation, commonly approximating generic class prototypes. Their utilization addresses sampling complexity issues inherent to purely sample-based approaches, resulting in improved convergence and benchmark performance.
Shortcomings
However, there is no free lunch. Relying on sample-proxy relations, relations between samples within a class can not be explicitly captured. This is exacerbated by proxy-based objectives optimizing for distances between samples and proxies using non-bijective distance functions. This means, for a particular proxy, that alignment to a sample is non-unique - as long as the angle between sample and proxy is retained, i.e. samples being aligned isotropically around a proxy (see thumbnail figure), their distances and respective loss remain the same. This means that samples lie on a hypersphere centered around a proxy with same distance and thus incurring the same training loss. This incorporates an undesired prior over sample-proxy distributions which doesn't allow local structures to be resolved well.
Representation-space Isotropy
By incorporating multiple classes and proxies (which is automatically done when applying proxy-based losses such as to training data with multiple classes), this is extended to a mixture of sample distributions around proxies. While this offers an implicit workaround to address isotropy around modes by incorporating relations of samples to proxies from different classes, relying only on other unrelated proxies potentially far away makes fine-grained resolution of local structures difficult. Furthermore, as training progresses and proxies move further apart. As a consequence, the distribution of samples around proxies, which proxy-based objectives optimize for, comprises modes with high affinity towards local isotropy. This introduces semantic ambiguity, as semantic relations between samples within a class are not resolved well, and intraclass semantics can not be addressed. However, a lot of recent work has shown that understanding and incorporating these non-discriminative relations drives generalization performance.
Contributions
To address this, we propose a novel method that
- introduces a principled Non-Isotropy Regularization-module () for proxy-based DML on the basis of class-conditioned normalizing flows,
- avoids the use of sample-to-sample relations, thus maintaining fast convergence speeds of proxy-based methods,
- has minimal impact of overall training time while signficantly and reliably improving generalization performance of proxy-based DML,
- consistently improves upon structures (such as Uniformity or feature variety) often related to better out-of-distribution generalization performance, as shown in multiple ablational studies.
Non-Isotropy Regularisation () for Proxy-based DML
To address the non-learnability of intraclass context in proxy-based DML, we have to address the inherent issue of local isotropy in the learned sample-proxy distribution .
Motivation
However, to retain the convergence (and generalization) benefits of proxy-based methods, we have to find a , whose optimization better resolves the distribution of sample representations around our proxy , without resorting to additional augmentations that move the overall objective away from a purely proxy-based one.
Assuming feature representations taken from the (pseudo-)metric presentation space spanned by a deep neural network and respective class proxy representations , we argue the following: Non-isotropy can be achieved by breaking down the fundamental issue of non-bijectivity in the used similarity measure (or equivalently the distance function ), which (on its own) introduces non-unique sample-proxy relations.
Consequently, we propose to enforce that each sample representation can be mapped by a bijective and thus invertible (deterministic) translation which, given some residual from some prior distribution , allows to uniquely translate from the respective proxy to .
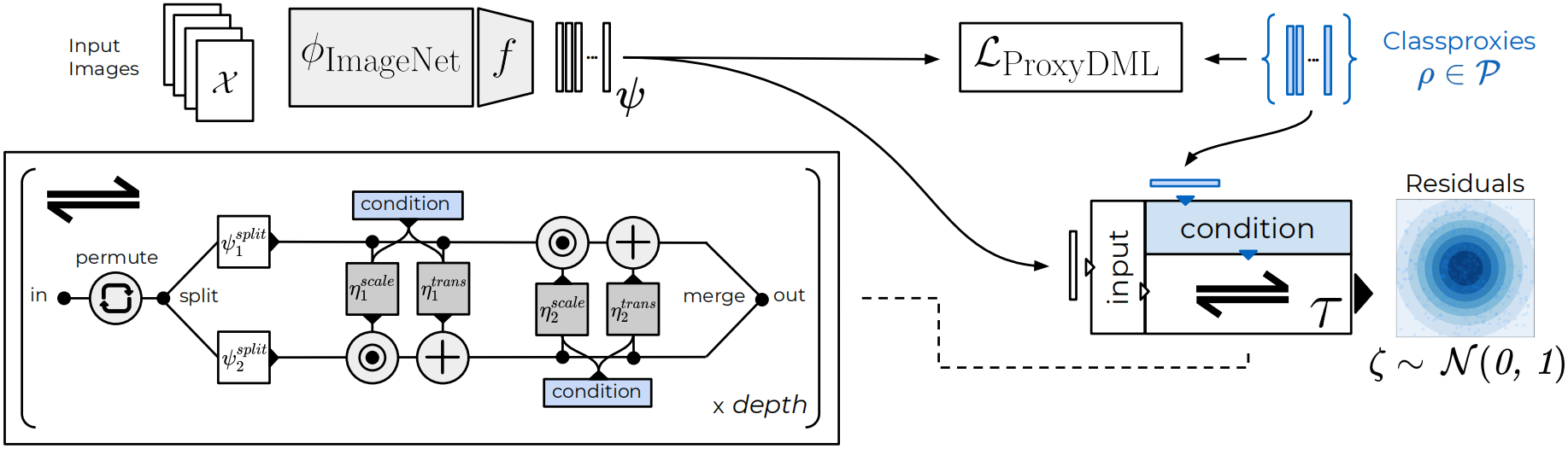
Normalizing Flows
Such invertible, ideally non-linear translations are naturally expressed through Normalizing Flows (NF), which can be generally seen as a transformation between two probability distributions, most commonly between simple, well-defined ones and complex multimodal ones. Normalizing Flows introduce a sequence of non-linear, but still invertible coupling operations as showcased via in our setup figure. Given some input representation , a coupling block splits into and , which are scaled and translated in succession with non-linear scaling and translation networks and , respectively. Note that following \cite{glow}, each network provides both scaling and translation values . Successive application of different then gives our non-linear invertible transformation from some prior distribution over residuals with explicit density and CDF (for sampling) to our target distribution.
By conditioning on respective classproxies , we can induce a new sample representation distribution as pushforward from our prior distribution of residuals which accounts for unique sample-to-proxy relations, and which we wish to impose over our learned sample distribution . This introduces our Non-Isotropy Regularization
In more detail, can be naturally approached through maximization of the expected log-likelihood over sample-proxy pairs , but under the constraint that each distribution of samples around a respective proxy, , is a pushforward of from our residual distribution . This gives
with Jacobian for translation and proxies , where denotes the class of sample . To arrive at above equation, we simply leveraged the change of variables formula
In practice, by setting our prior to be a standard zero-mean unit-variance normal distribution , we get
i.e. given sample representations , we project them onto our residual space via and compute our -objective. By selecting suitable normalizing flows such as GLOW, we make sure that the Jacobian is cheap to compute.
In applying , we effectively enforce that all sample representations around each proxies are defineable through unique translations. This means that our underlying Normalizing Flow retains implicit knowledge about class-internal structures without our overall setup having to ever rely on sample-to-sample relations!
Experiments
By applying to various strong proxy-based DML objectives such as ProxyNCA, ProxyAnchor or SoftTriplet, we find consistent improvements in generalization performance across all methods and in particular across all kinds of benchmarks.
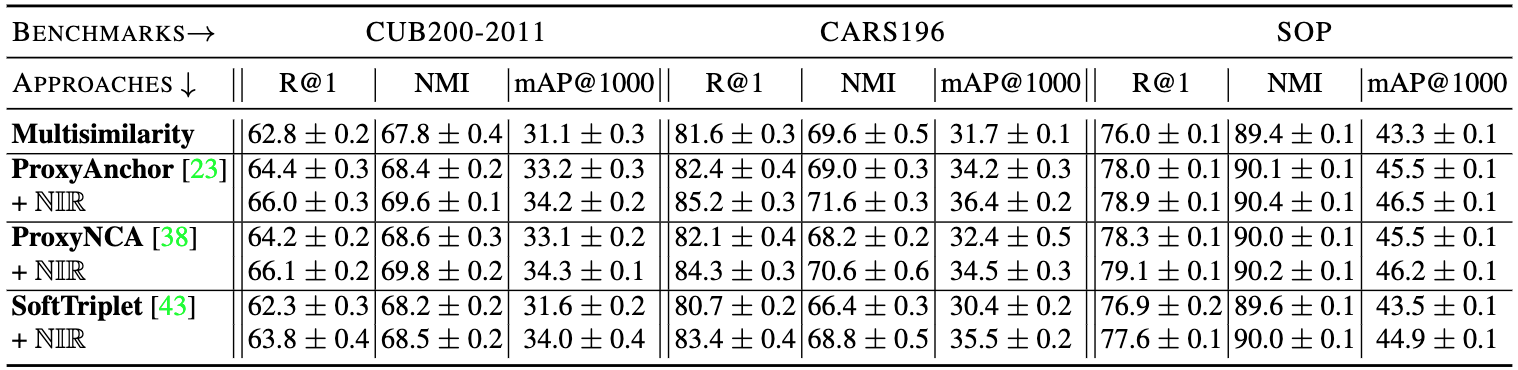
In addition to that, these performance improvements come at no relevant impact to training time, as only operates in the much lower-dimensional representation space. Furthermore, and importantly, convergence speeds are retained and in parts even improved!
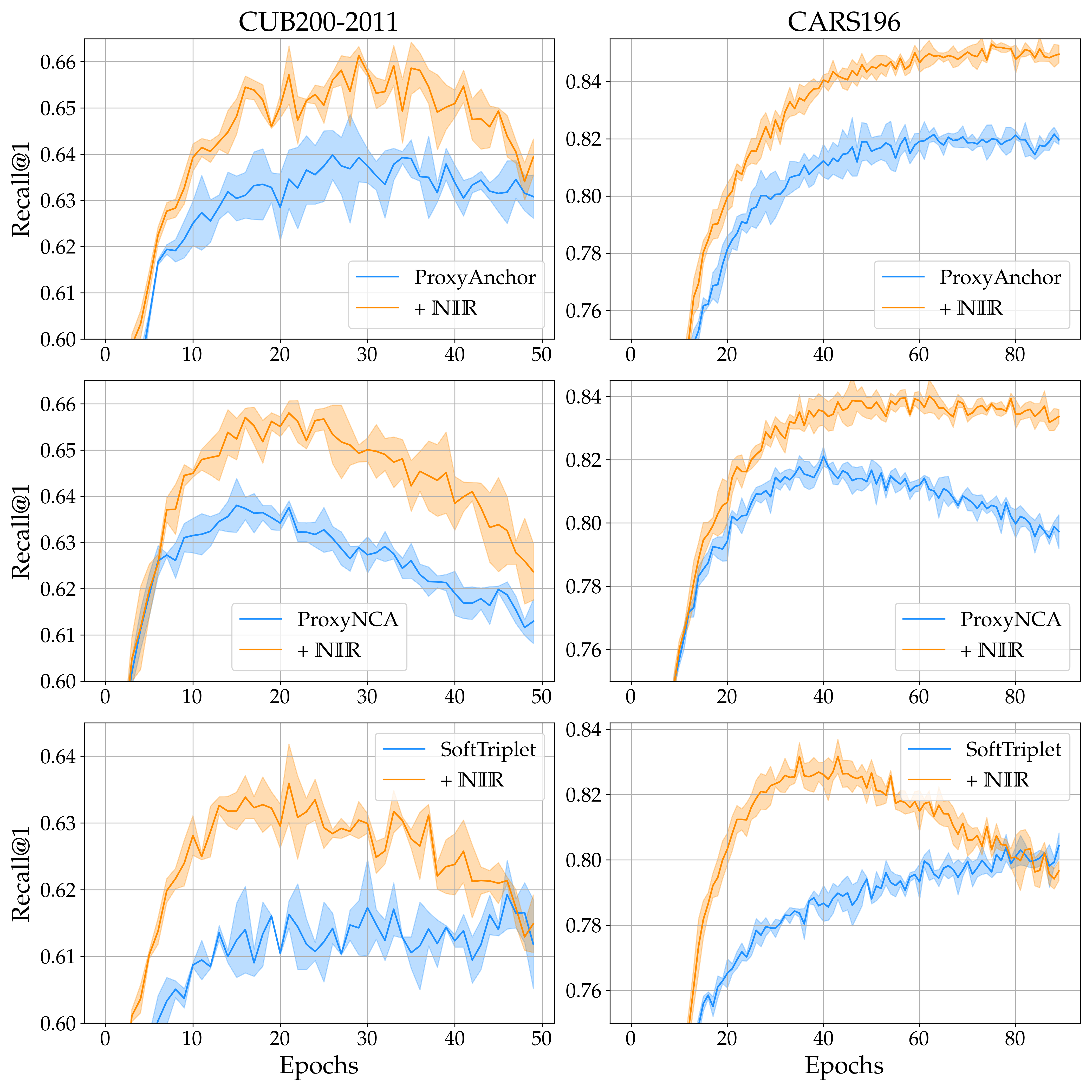
Finally, when evaluating -regularized objectives, we find consistent increases in feature space uniformity () and feature variety (), reduced overclustering () as well as higher variability in class-cluster sizes . While the former three are commonly linked to better generalization performance, the latter provides nice additional support on encouraging more class-specific sample-distributions to be learned!