Parameter-efficient finetuning (PEFT) has become ubiquitous to adapt foundation models to downstream task requirements while retaining their generalization ability. However, the amount of additionally introduced parameters and compute for successful adaptation and hyperparameter searches can explode quickly, especially when deployed at scale to serve numerous individual requests. To ensure effective, parameter-efficient, and hyperparameter-robust adaptation, we propose the ETHER transformation family, which performs Efficient fineTuning via HypErplane Reflections. By design, ETHER transformations require a minimal number of parameters, are less likely to deteriorate model performance, and exhibit robustness to hyperparameter and learning rate choices. In particular, we introduce ETHER and its relaxation ETHER+, which match or outperform existing PEFT methods with significantly fewer parameters (~- times lower than LoRA or OFT) across multiple image synthesis and natural language tasks without exhaustive hyperparameter tuning. Finally, we investigate the recent emphasis on Hyperspherical Energy retention for adaptation and raise questions on its practical utility. The code is available at https://github.com/mwbini/ether.
Motivation
Large-scale foundation models offer impressive capabilities, but their massive parameter counts pose challenges for affordable and scalable adaptation. Parameter-efficient finetuning (PEFT) techniques, especially those leveraging lightweight transformations, have emerged as effective solutions. These methods finetune on smaller datasets to adapt to downstream tasks, without incurring significant inference latency, parameter counts, or compromising the costly pretraining. However, striking the right balance between adaptation and retention of foundational model abilities often requires expensive hyperparameter tuning.
In this work, we propose ETHER (Efficient Finetuning via Hyperplane Reflections) - a new family of multiplicative weight transformations that are efficient in parameter count while preserving model abilities and being robust in convergence and learning rate choices.
ETHER and ETHER+
ETHER. ETHER sets up weight transformations as hyperplane reflections using the Householder transformation:
These reflections keep the distance to the identity matrix constant, minimizing the risk of divergence from the pretrained model during finetuning. This allows for a low number of extra parameters and the use of high learning rates, resulting in learning rate robustness and fast convergence.
ETHER+. While ETHER has these benefits, the strong transformation strength may not be suitable for more nuanced tasks. To address this, the paper proposes ETHER+, a relaxed variant of the Householder transformation:
ETHER+ allows for interactions between two distinct hyperplanes, which can weaken or cancel each other out to provide more nuanced weight adjustments. Importantly, the transformation distance remains bounded, still minimizing the risk of diverging from the pretrained model.
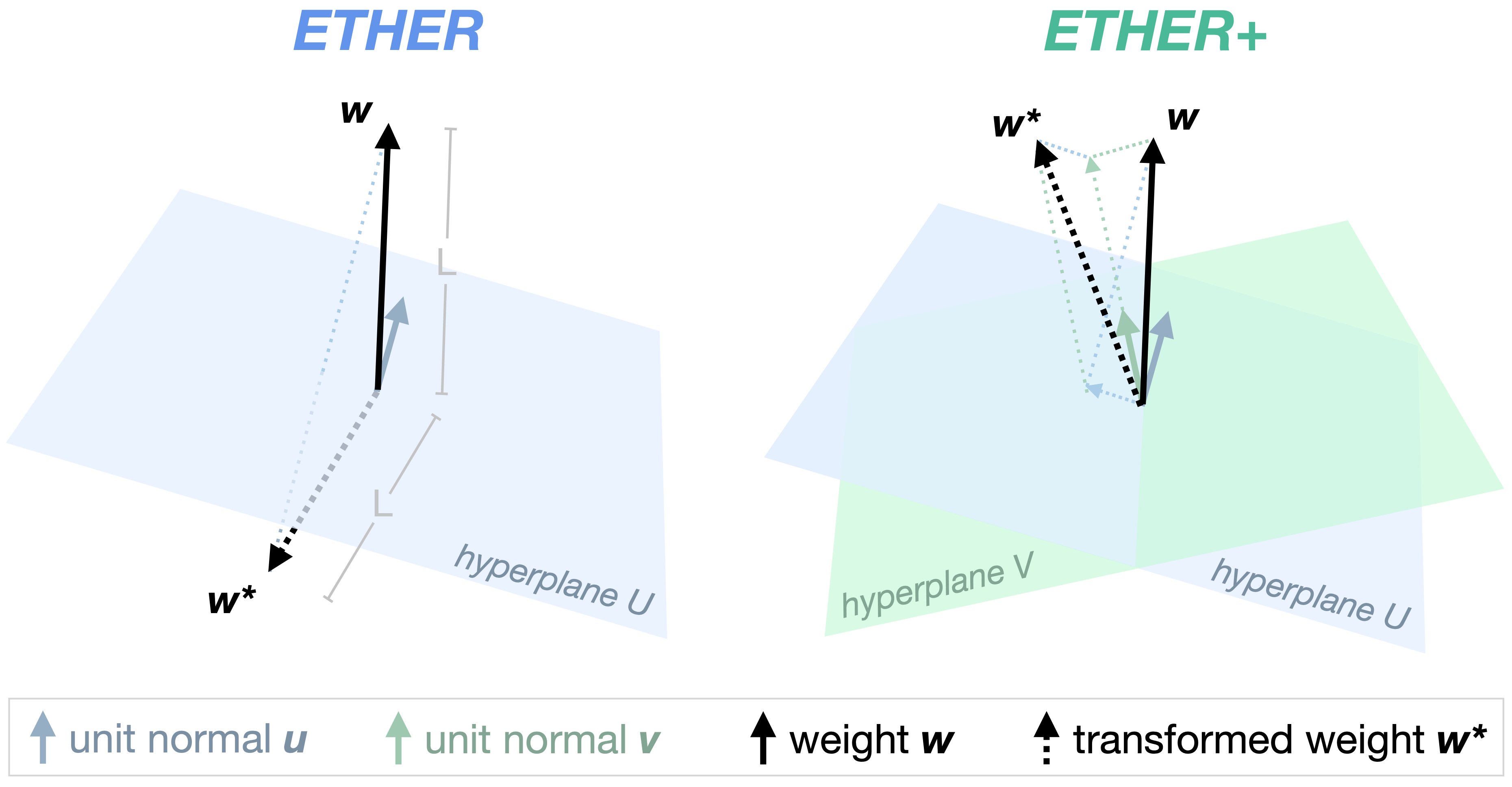
Overall, ETHER leverages hyperplane reflections for efficient and stable finetuning, while ETHER+ relaxes the constant distance to enable more flexible transformations when needed, while retaining the core benefits of the approach.
Why to use ETHER: Intriguing Properties
The ETHER and ETHER+ methods exhibit several intriguing properties that make them attractive for practical finetuning tasks:
Non-Deteriorating Nature. Both ETHER and ETHER+ are upper-bounded in their possible perturbation over the pretrained weight matrices, ensuring suitable results for most hyperparameter choices. We qualitatively visualize this by perturbing Stable Diffusion with transformations of different distance (below, left), finding that ETHER and ETHER+ perturbed models still retain semantics despite noticeable changes, unlike the catastrophic deterioration of an unbound method like OFT.
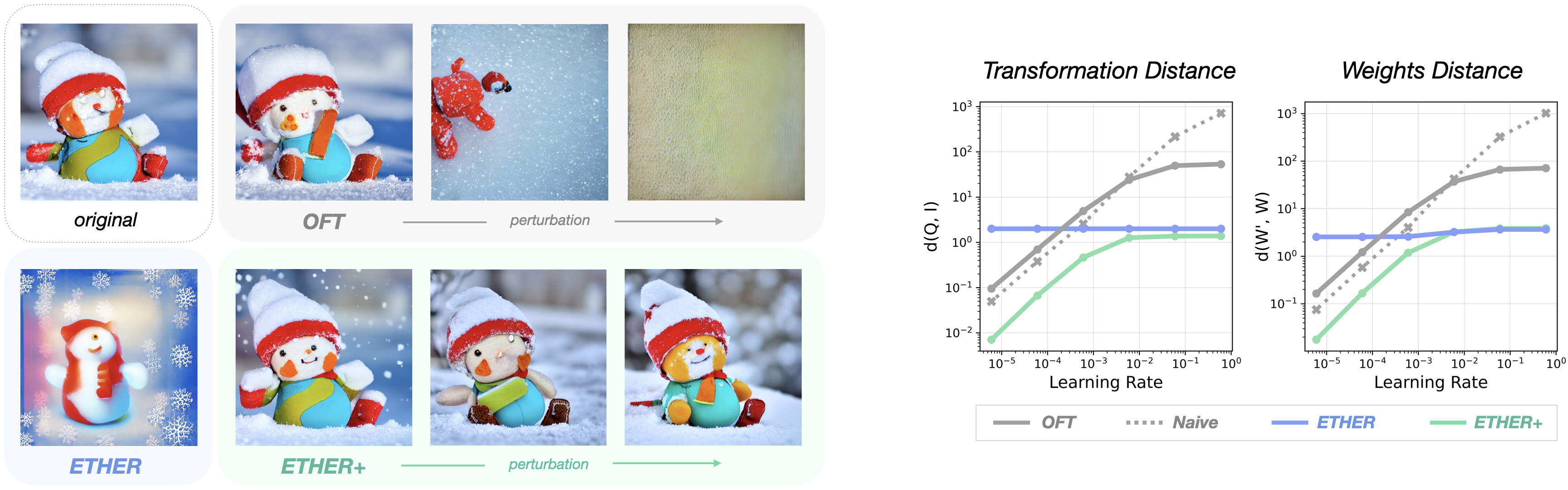
Learning Rate and Hyperparameter Robustness. The non-deteriorating nature of ETHER and ETHER+ results in learning rate robustness during finetuning, where training stability becomes much less dependent on the choice of learning rate. ETHER+ can achieve fast convergence with learning rates covering multiple magnitudes, while non-ETHER methods exhibit significant performance drops at high learning rates.
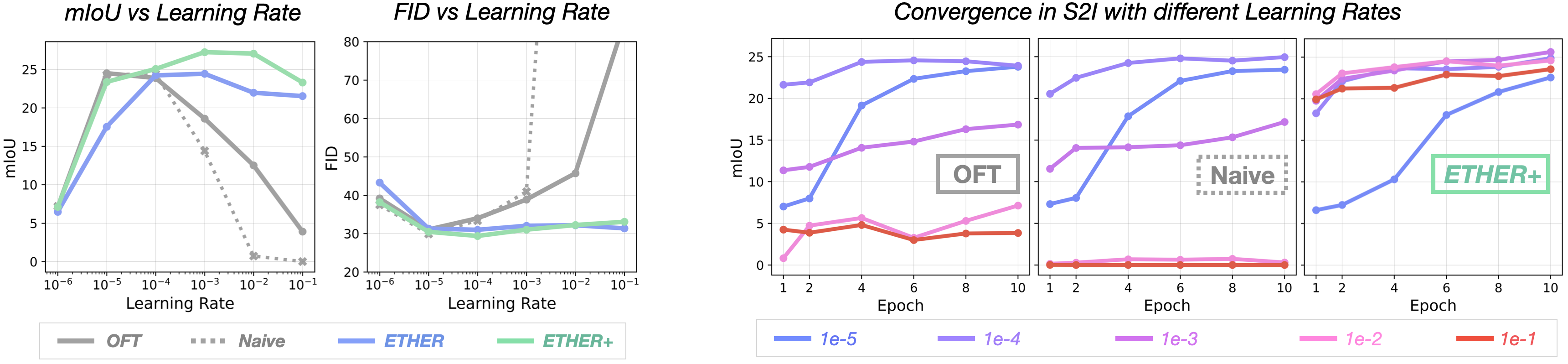

Parameter Efficiency. ETHER-based methods, consisting in a search for optimal reflection hyperplanes, are highly parameter-efficient, using significantly fewer parameters than other finetuning approaches like OFT and LoRA. For example, when finetuning Stable Diffusion, ETHER and ETHER+ use 120 times and 30 times fewer parameters than OFT, respectively.
The bounded perturbation, learning rate robustness, and parameter efficiency of ETHER and ETHER+ make them attractive practical finetuning methods.
Speeding-up Multiplicative Finetuning with Block-parallel Scheme
Multiplicative finetuning techniques like ETHER introduce additional computational load through extra matrix multiplications. To mitigate this issue, the paper proposes the usage a block-diagonal formulation of ETHER.
In this block-diagonal structure, each block on the diagonal of the transformation matrix only affects a sub-block of the weight matrix . As a result, the full weight transformation can now be separated into smaller block-specific operations. This significantly increases the training speed by reducing the overall number of computations from to . In addition, each of this block operations can now be fully parallelized, further speeding-up the method.
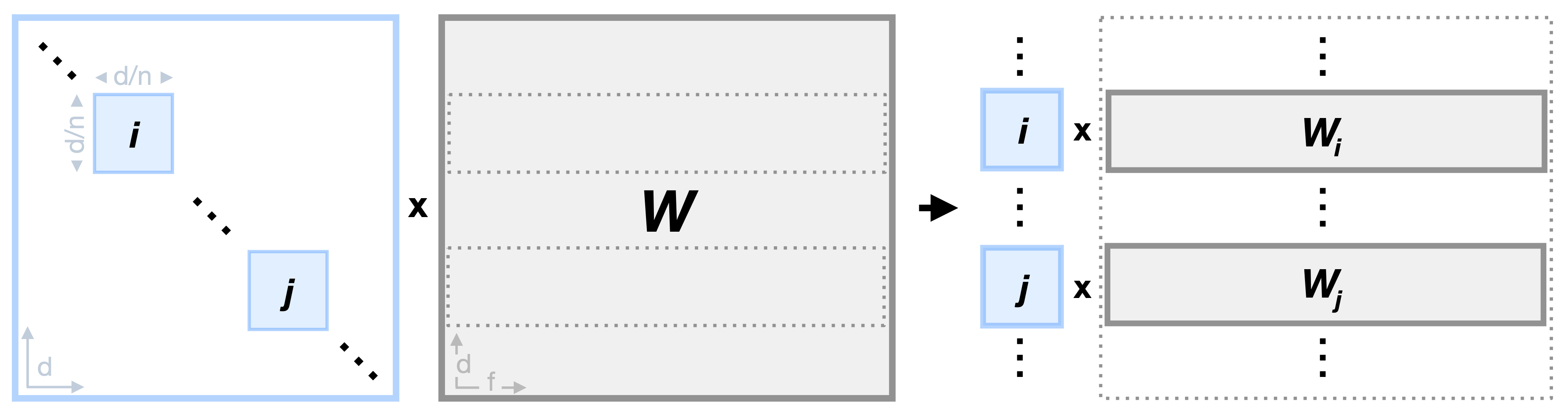
Importantly, in ETHER transformations the total number of trainable parameters remains constant regardless of the number of blocks n, unlike block-diagonal OFT where higher block counts decreased adaptation performance. Instead, the block-parallel ETHER is found to maintain consistent performance even with increasing block counts, allowing for an improved computational footprint with negligible performance impact.
Multiplicative Finetuning needs Hyperspherical Energy Retention?
OFT links the finetuning stability and performance obtained by transforming the weights via matrix-multiplication to the orthogonality of the transformations, and a consequently unaltered hyperspherical energy (HE). To test this assumption, we have included an OFT control baseline (Naive), which does not utilize orthogonality constraints.
Our experiments do not show significant differences in terms of performance and training stability, suggesting that such properties stem from the multiplicative finetuning approach rather than the underlying HE retention.
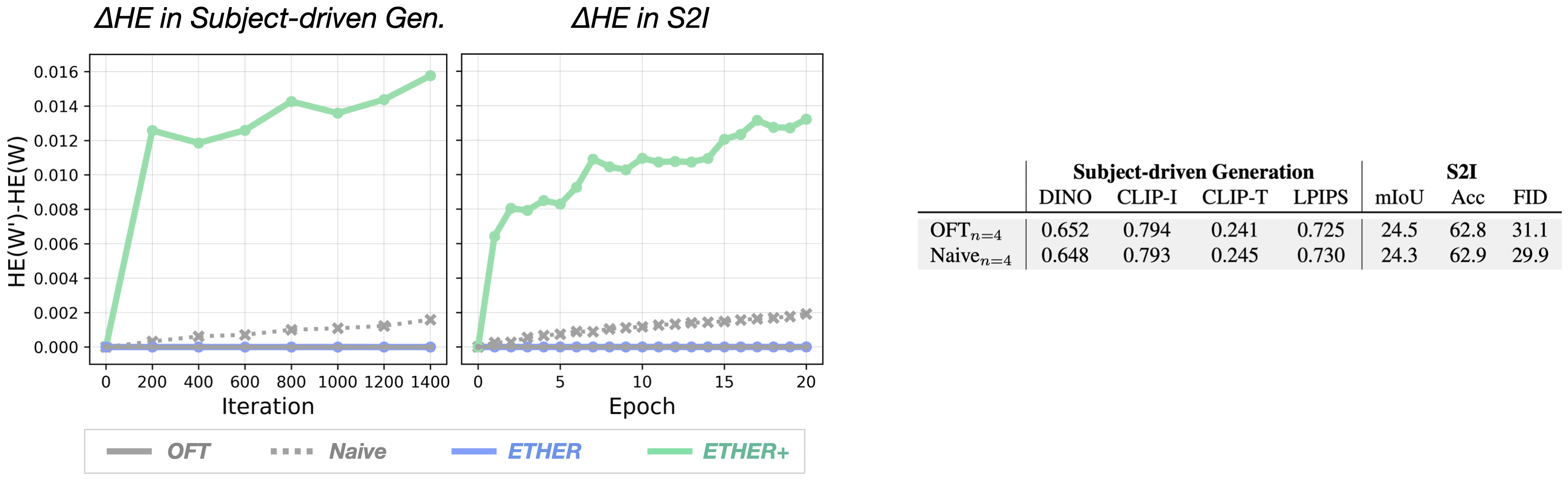
This evidence diminishes the role of the HE and instead emphasizes the greater importance of the Euclidean distance, establishing the ETHER family as a favorable option in multiplicative finetuning settings.
Benchmark Experiments
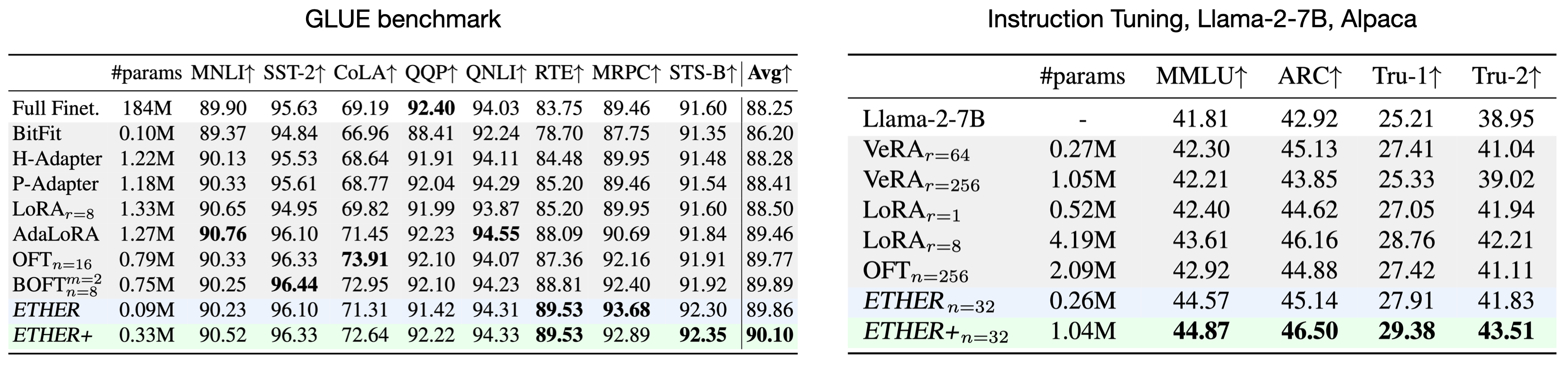
We tested our method on generative model adaptation, with a focus on subject-driven image synthesis and controllable image synthesis, and on language model adaptation, looking at both natural language understanding and instruction tuning.
Subject-driven generation.

Controllable generation.

Language Model Adaptation.
Want to know more?
For more details (additional tables, ablations, further considerations) have a look at the full paper! Do you want to test the finetuning method yourself? The code is available here.